Equation of SHM

Electrons moving with different speeds enter a uniform magnetic field in a direction perpendicular field. They will move along circular paths, time periods of rotation will be :

The $\mathrm{x}-\mathrm{t}$ graph of a particle undergoing simple harmonic motion is as shown in the figure.

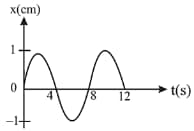
The acceleration of the particle at $\mathrm{t}=\frac{4}{3}\mathrm{ }\mathrm{s}$ is

Two particles are performing SHM in same phase. It means that:
 

A particle of mass $\text{'}m\text{'}$ is under an influence of a force $\overrightarrow{F}=-k\overrightarrow{x}+{\overrightarrow{F}}_0.$ The particle when disturbed will oscillate $\_\_\_$

Ratio of maximum acceleration to the maximum velocity of a simple harmonic oscillator is

A particle executing simple harmonic motion has a maximum speed of $40 \mathrm{m}·{\mathrm{s}}^{-1}$ and maximum acceleration of $60 \mathrm{m}·{\mathrm{s}}^{-2}$. The period of oscillation is

The displacement of a simple harmonic motion of amplitude $6 \mathrm{cm}$ when its kinetic energy is equal to its potential energy is

Match the following entries in column-I and column-II with respect to an oscillating spring-block system:

A simple harmonic oscillation is represented by $x=A\cos \left(\omega t+\frac{\pi }{4}\right).$ Its speed is maximum when $\text{'}t\text{'}$ equals

A particle of mass $0.4 \mathrm{kg}$ executes simple harmonic motion of amplitude $0.4 \mathrm{m}.$ When it passes through the mean position, its kinetic energy is $256\times {10}^{-3} \mathrm{J}.$ If the initial phase of the oscillation is $\frac{\mathrm{\pi }}{4},$ then the equation of its motion is ______

Thus, simple harmonic motion (SHM) is not any periodic motion but one in which displacement is sinusoidal function of time.

Two SHM’s are respectively by $y=a_1\sin (\omega t-kx)$ and $y=a_2\cos (\omega t-kx).$ The phase difference between the two is

When a spring-mass system vibrates with simple harmonic motion, the mass in motion reaches its maximum velocity when its acceleration is _____ (maximum\minimum).

A block of mass $\mathrm{m}=4 \mathrm{kg}$ undergoes simple harmonic motion with amplitude$\mathrm{A}= 6 \mathrm{cm}$ on the frictionless surface. Block is attached to a spring of force constant $k=400 \mathrm{N} {\mathrm{m}}^{-1}$ . If the block is at$\mathrm{x}=6 \mathrm{cm}$ at time $t=0$ and equilibrium position is at $x=0$ then the blocks position as a function of time (with x in centimetres and t in seconds) ?

A mass of $36 \mathrm{kg}$ is kept vertically on the top of a massless spring. What is the maximum compression of the spring if the spring constant is $15000 \mathrm{N}/\mathrm{m}$. Assume $\mathrm{g} = 10\mathrm{m}/{\mathrm{s}}^2$.

Suppose a particle P is moving uniformly on a circle of radius A with the angular speed $\omega$ . The sense of rotation is anticlockwise. If the $t=0$ , it  makes an angle of $\varphi$ with the positive direction of the x-axis. In time $t$, it will cover a further angle $\omega t$.What is the projection of position vector on the X-axis at time $t$.

If we tie a stone to the end of a string and move it with a constant angular speed in a horizontal plane about fixed point, the stone would perform a : 

If the particle is moving in circular motion under SHM, then its x-projection is depending upon

The x-projection for a certain particle in circular motion under SHM with period of $2 \mathrm{s}$, amplitude of oscillation is $2 \mathrm{m}$ and initial phase of $\frac{\mathrm{\pi }}{2}$ is

Which of the following conditions is not sufficient for S.H.M. and why?